The Statistical Learning Framework
Let’s first describe a formal model capturing statistical learning tasks.
The Learner’s Input
-
Domain set
: A set of objects that we wish to label. Usually, this domain points are represented by a vector of features (e.g., several papayas represented by their color and softness).
-
Label set
: For current discussion,
is restricted to a two-element set,
or
(e.g., whether the papaya is tasty or not).
-
Training data
: A finite sequence of pairs in
; that is, a sequence of domain points and their labels.
How the Training Data 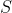 is Generated
is Generated
-
We assume that each instance
is sampled according to a probability distribution
-
For current discussion, assume that there is a "correct" labeling function
such that
for all
.
The Learner’s Output
-
The learner does not know anything about
and is required to learn
-
The learner should output a prediction rule (function)
. The function is also called predictor, a hypothesis, or a classifier.
Measures of Success
-
The error of a classifier is defined as the probability that it does not predict the correct label of a randomly sampled (according to
) data point.
-
Formally, the error of the classifier
is defined as
.
-
The notation
assigns a probability determining how likely it is to observe a point
, where
is an event.
-
In other words, with respect to the distribution
and the correct labeling function
, the error of such
is the probability of a randomly sampled example
belonging to the set
-
is also called the generalization error, the risk, the true error of
-
The letter
is used since we view the error as a loss of the learner.